1.3 统计与概率
1.3.1 统计与概率简介
随机振动信号似乎很难定量描述。仅仅是回答“它有多大”这个问题就具有挑战性。本节介绍了一些量化随机信号的方法,包括统计量(例如平均值)和概率分布(例如正态曲线)。该课程还涵盖产品设计方面的应用,例如公差和疲劳分析。
1.3 统计与概率
1.3.1 统计与概率简介
随机振动信号似乎很难定量描述。仅仅是回答“它有多大”这个问题就具有挑战性。本节介绍了一些量化随机信号的方法,包括统计量(例如平均值)和概率分布(例如正态曲线)。该课程还涵盖产品设计方面的应用,例如公差和疲劳分析。
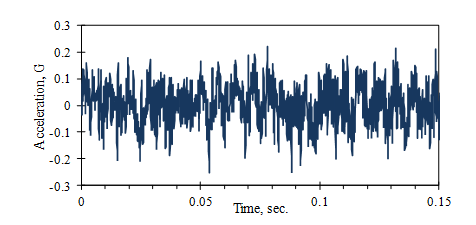
图1:随机振动信号(120 km/h行驶车辆的车底的加速度)
在本节中,假设连续振动信号x(t)已被数字化为用于分析的数字序列xn,n=1,…,N。
1.3.2 均值
用于描述随机变量的单个数字的统计测量被称为点估计。讨论仅限于时间上平稳的随机变量;也就是说,在足够长的时间内进行平均时,点估计值是稳定的。
均值。一组数字xn,n=1,…,N的平均(或“算术平均”)值,由下式给出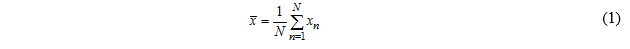
其中,上横线是此处使用的平均值的记法。
对于许多振动信号,例如图1所示的信号,平均值接近零。这是因为振动围绕固定位置在正方向和负方向上均等地发生。请注意,振动传感器的电子元件通常会滤除振动的“ DC”分量——其为平均值的电气等效值。
1.3.3 均方值
均方值 一组数字xn,n=1,…,N的均方值,由下式给出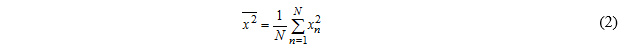
均方值测量信号的平均强度或功率。图2绘出了图1中振动信号的平方并示出了均方值。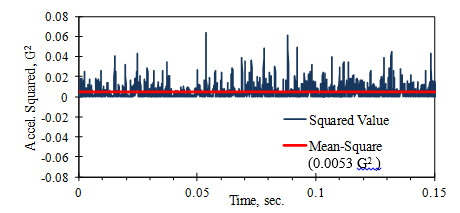
图2
对于均值为零的随机信号,均方值是两个信号求和时可以相加的量。通过考虑两个随机变量A和B的和可以看出这点。(A+B)的平方由(A+B)2=A2+2A·B+B2给出。如果A和B是均值为零的独立随机变量,则A·B的均值是零。然后,总和的均方值等于均方和(均值为零)。
1.3.4 方差
方差 平均值为μ的一组数字xn,n=1,…,N的方差为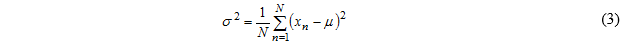
如果已经使用式1求出这组数字的平均值,则方差为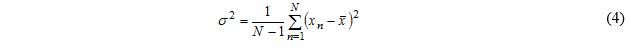
求和符号之前分母中的值是求和中使用的独立值(或自由度)的数量。由于是根据与式4中使用的相同的一组数字来计算的,所以式4求和的最后一项的值是预先确定的,因此求和中独立值的数量为N–1。
对于均值为零的振动信号,方差等于均方值。一般地,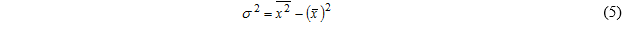
当对独立随机变量求和时,方差相加(即使均值非零)。
1.3.5 标准差
标准差 一组数字的标准偏差xn,n=1,…,N给出为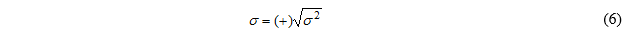
标准差是信号均值附近信号变异性的度量。对于均值为零的振动信号,标准差等于信号的RMS(均方根)值。回到图1和2中使用的振动信号。参照图1和图2,标准差和RMS的值都为0.073G。
方差和标准差在确定统计量的置信区间(或相反地,不确定性)中起重要作用。在“置信区间”课程中将对此进行进一步讨论。
1.3.6 偏度
偏度 一组数字xn,n=1,…,N的偏度由下式给出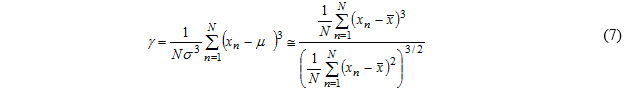
偏度是信号围绕其均值的不对称扩展的度量。它是均值的均立方偏差除以标准偏差的立方的比率。因此,它是无量纲的。对于具有正态分布的随机变量,偏度为零(请参见关于正态(高斯)分布的课程)。
图3示出了在飞行中的飞机的蒙皮的外部测得的湍流压力。压力相对于均值的负波动要大于正波动,从而使偏度的值为γ=-0.32(均值为-0.03kPa,标准差为1.08kPa)。请注意,压力的真实均值(大气压patm)已通过电子方式从信号中取出,因此,所测得的信号实际上为(p–patm),均值接近零。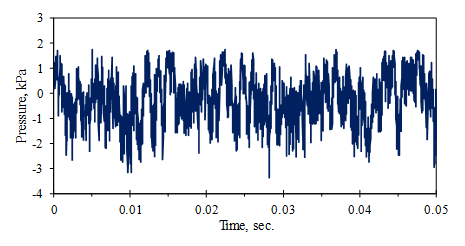
图3.在0.5马赫时在飞机蒙皮外部测得的湍流压力
1.3.7 峭度
峭度 一组数字xn,n=1,…,N的峭度由下式给出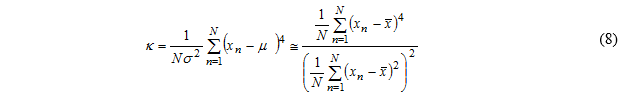
峭度是信号偏离其均值的均四次方除以标准差的四次方的量度。因此,它是无量纲的。对于具有正态分布的随机变量,峭度的值为3(请参见关于正态(高斯)分布的课程)。图3所示的湍流压力信号的峭度值为2.6。
应当注意,某些计算机程序计算超出峭度K-3值计算。正态分布的超峭度为零。
1.3.8 概率分布简介
当需要对随机变量进行更详细的描述时,除了上面的“统计”课程所涵盖的点估计之外,还可以使用概率密度函数(PDF)。PDF是不同水平的变量的概率直方图。当信号被数字化为一系列值xn,n=1,…,N时,它们将被视为信号样本集。概率直方图是通过对样本数m进行计数来计算的,样本数m为信号幅值全范围中的一分组箱中的样本的数目,如图4所示,其中使用了来自图1的车辆振动数据。绘出各分组箱的样本分数m/N与分组箱水平关系的条形图(这里箱宽度为Δx=0.02G)。这样,所有分组箱对应的数目分数的总和等于1,但它们的量值的范围取决于Δx的值。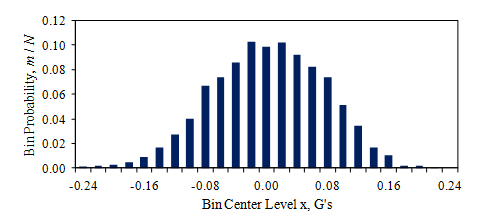
图4.图1所示的汽车振动信号的直方图
概率密度是通过在每个仓将样本的数量分数除以箱宽度来计算,Δx:PDF=m/(NΔx)。这在图5a中绘制为线图。该PDF还可以通过除以标准差进行归一化z=(x–μ)/σ,如图5b所示。这些被称为样本的PDF。真PDF在N→∞,分组箱数→∞(分组箱大小变为无穷小)时取到。两种情况下,PDF曲线下的面积都是1。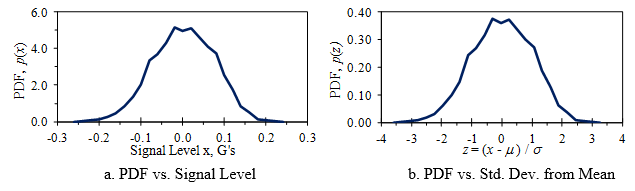
图5.图1所示的振动信号的PDF示例。
以下课程考察了一些理想的统计分布的PDF。对于这些分布,PDF可以描述为振幅x的连续函数,并且在理解随机振动分析方面起着重要作用。

欢迎您关注VR公众号!
